|
|
|
- Waveguide
-
|
|
See the online cavity
resonance calculator here.
Click
here
to go to waveguide selection chart.
|
Rectangular
Waveguide |
|
Cutoff
Frequency |
| The lower cutoff frequency (or
wavelength) for a particular mode in rectangular
waveguide is determined by the following
equations:
  (Hz) (Hz)
 (m) (m)
| where |
a=
b=
m=
n=
e
=
m
= |
Inside width
Inside
height
Number of ½-wavelength variations of
fields in the "a" direction
Number of
½-wavelength variations of fields in the "b"
direction
Permittivity
Permeability | |
| TE
(Transverse Electric) Mode |
| The TE10 mode is the
dominant mode of a rectangular waveguide with
a>b, since it has the lowest attenuation of all
modes. Either m or n can be zero, but not
both.

End View
(TE10)

Side View
(TE10)

Top View
(TE10)
____ Electric field
lines
_ _
_ Magnetic field lines |
| TM
(Transverse Magnetic) Mode |
| For TM modes, m=0 and n=0 are not
possible, thus, TM11 is the lowest
possible TM mode.

End View
(TM11)

Side View
(TM11)
____ Electric field
lines
_ _
_ Magnetic field
lines | | |
|
Circular Waveguide |
|
TE
(Transverse Electric) Mode |
 |
| The lower cutoff frequency (or
wavelength) for a particular TE mode in circular
waveguide is determined by the following
equation:
 (m), (m),
where p'mn
is
| m |
p'm1 |
p'm2 |
p'm3 |
| 0 |
3.832 |
7.016 |
10.174 |
| 1 |
1.841 |
5.331 |
8.536 |
| 2 |
3.054 |
6.706 |
9.970 | |
|
TM
(Transverse Magnetic) Mode |
| The lower cutoff frequency (or
wavelength) for a particular TM mode in circular
waveguide is determined by the following
equation:
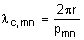 (m), (m),
where pmn
is
| m |
pm1 |
pm2 |
pm3 |
| 0 |
2.405 |
5.520 |
8.654 |
| 1 |
3.832 |
7.016 |
10.174 |
| 2 |
5.135 |
8.417 |
11.620 | | | |
|